Sigmoid Function

$sigmoid(Wx+b)=\frac{1}{1+e^{-(Wx+b)}}$
선형 회귀에서와 비슷하게, 가중치와, 편향을 찾는게 목표.

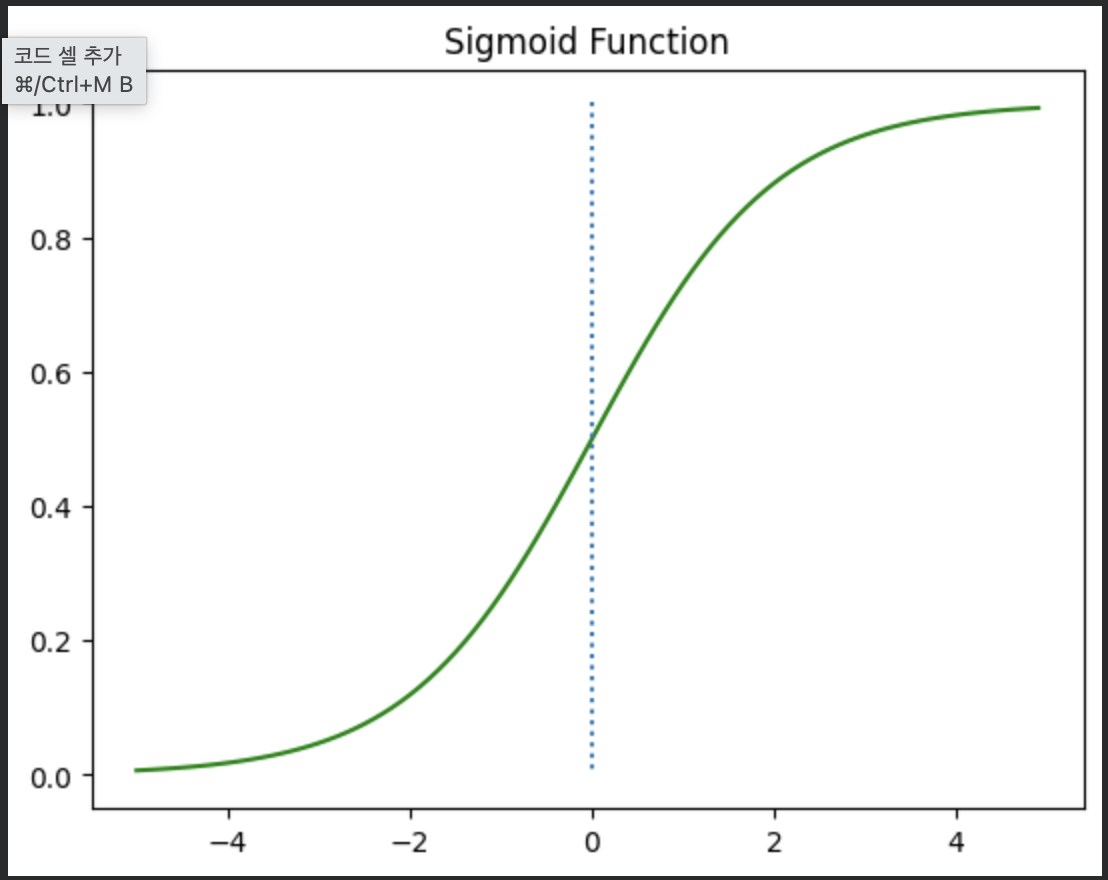
$-1<sigmoid(x)<1$ \lim_{x \to \infty}{sigmoid(x)}=1 $$$$ \lim_{x \to -\infty}{sigmoid(x)} = -1

W 바꿔보기

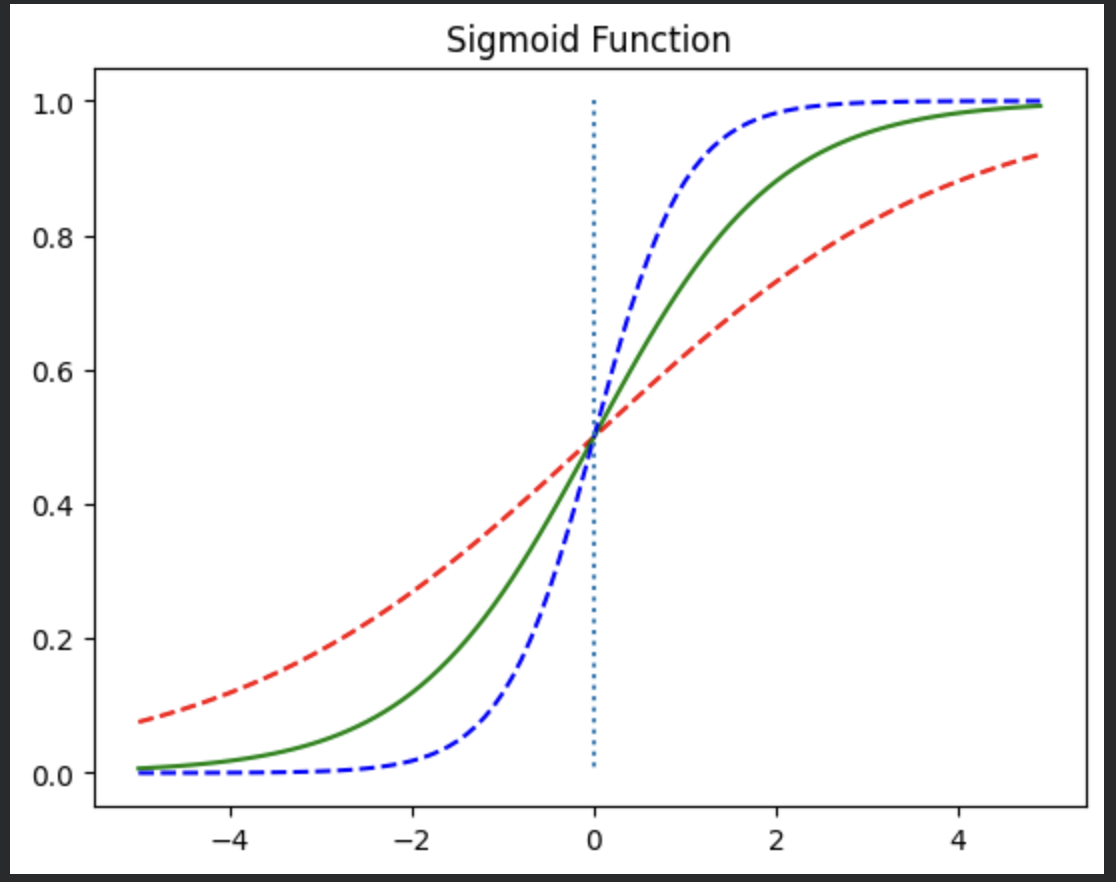
W값이 클 수록 그래프의 경사가 심해짐

b 바꿔보기

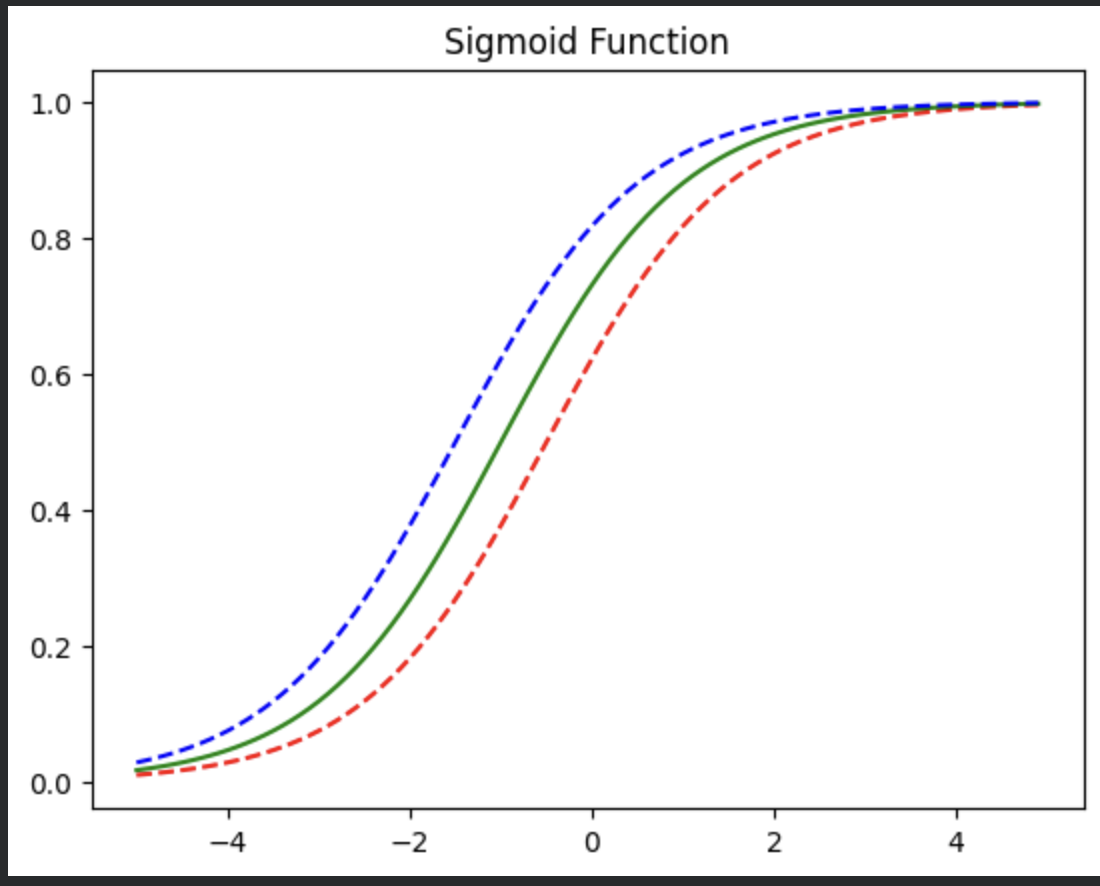그래프의 x축 이동

Sigmoid 비용 함수 - MSE(Mean Square Error)?

$cost(W,b)=\frac{1}{n}{\sum }_{i=1}^n[y^{(i)}-H(x^{(i)}){]}^2$
$H(x)=sigmoid(Wx+b)$

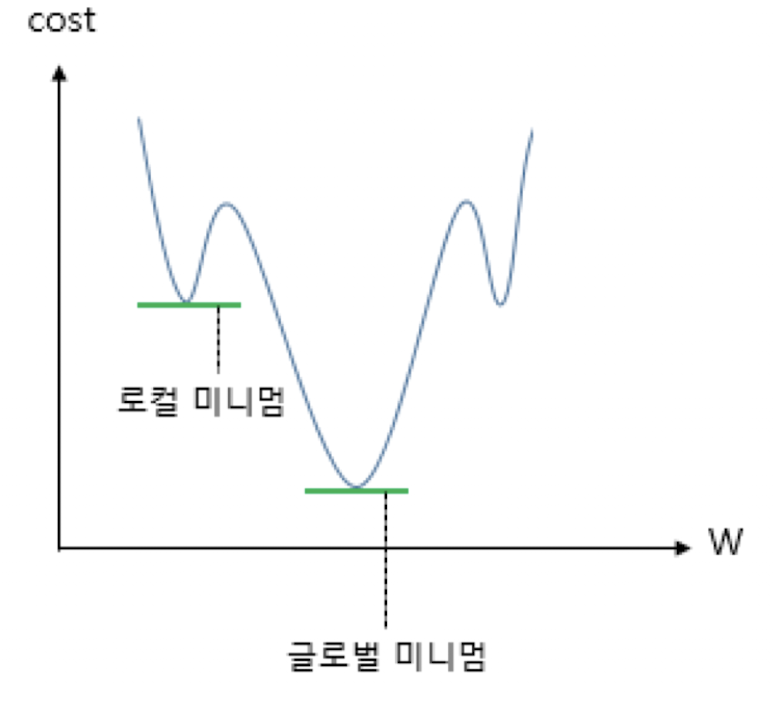
미분한다고 해도 최소값을 찾을 수 있는게 아니라서 이거 안씀.

Sigmoid 비용 함수 - 크로스 엔트로피 함수

$cost(H(x),y)=\{\begin{array}{l}-\log (H(x))\\ -\log (1-H(x))\end{array}$

$$cost(W)=-\frac{1}{n}[y^{(i)}\log (H(x^{(i)}))+(1-y^{(i)})\log (1-H(x^{(i)}))]$$

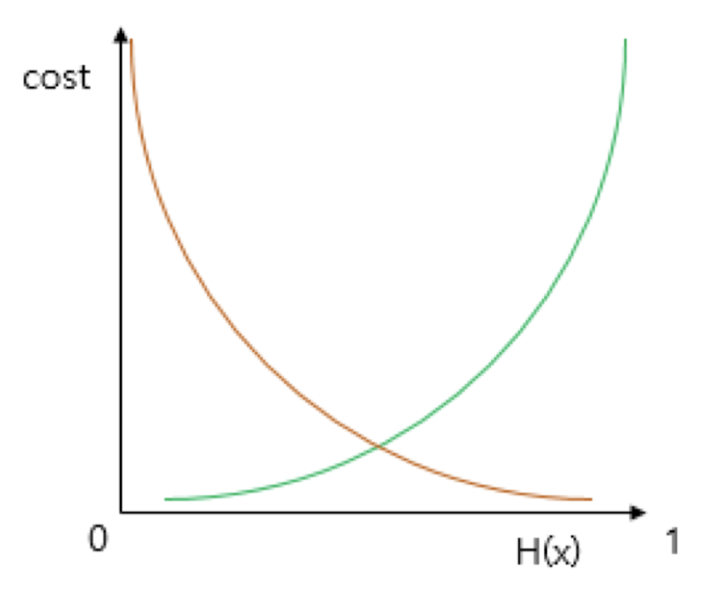
y = 실제 결과값(1 or 0)

문제점

Not zero-centered. > 평균이 0.5 > 항상 양수 출력 > 출력의 가중치 합이 입력의 가중치 합보다 커질 가능성이 큼(편향 이동(Bias Shift)) > 레이어를 지날 때마다 분산이 계속 커져 출력이 수렴해 기울기 소실 문제가 일어날 수도