Activation Function

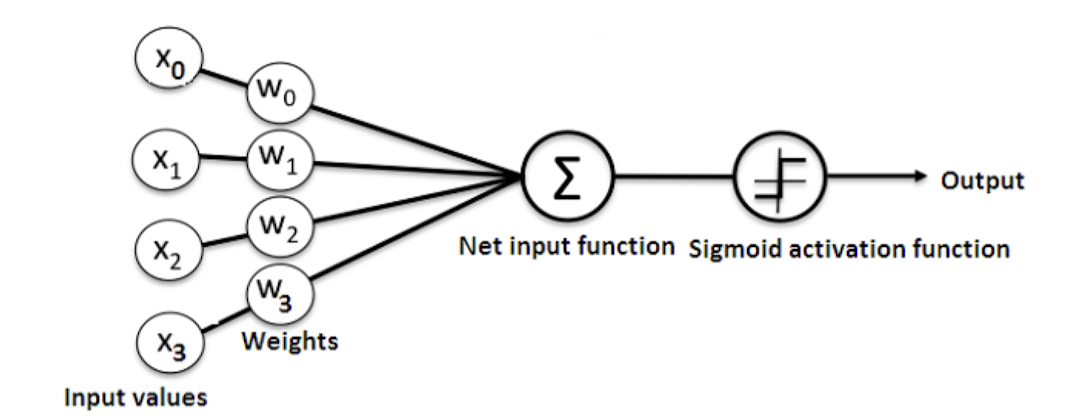
뉴런에서 출력값을 변경시키는 함수.
Nonlinear function : 활성화 함수는 비선형 함수이다.

선형 함수로는 은닉층을 여러번 추가하더라도 1회 추가한 것과 등가이다.
그러므로 은닉층에 선형 함수를 사용한다면, 중간중간에 비선형 함수를 끼워줘야함.

문제	활성화 함수
Binary Classfication	Sigmoid
Multi-class Classification	Softmax
Regression	없음.

스탠포드 대학교의 딥 러닝 강의(cs231n)에서는 ReLU를 먼저 시도해보고, 그 다음으로 LeakyReLU나 ELU같은 ReLU의 변형들을 시도해보며, Sigmoid는 사용하지 말라고 권장함.

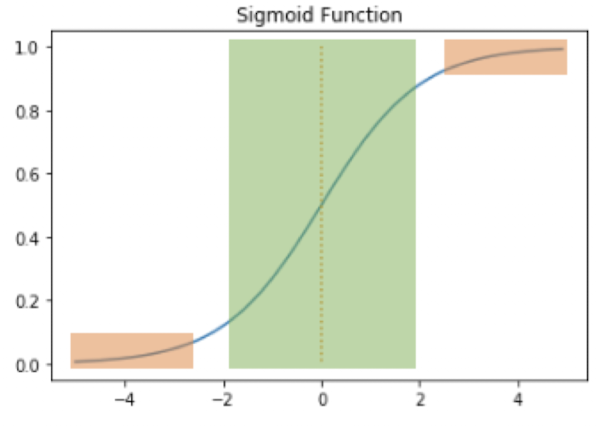
Sigmoid Function and Vanishing Gradients

선형 회귀의 일반적인 학습 과정

1. 인공 신경망은 입력에 대해서 순전파 연산
2. 순전파 연산을 통해 나온 예측값과 실제값의 오차를 Cost Function 통해 계산
3. 오차(Cost)를 미분하여 Gradient 구하고,
4. 역전파 수행
5. (Zeroing Gradients)

원본 링크

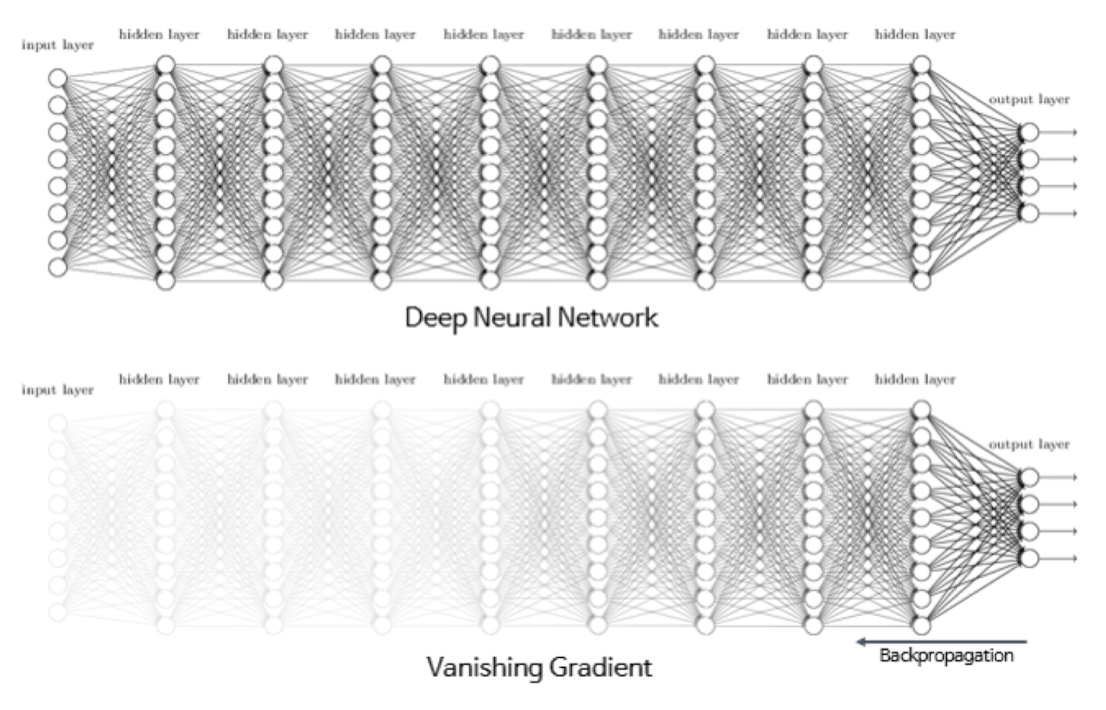
Vanishing Gradients

역전파 과정에서 0에 가까운 아주 작은 기울기가 곱해지게 되면, 앞단에는 기울기가 잘 전달되지 않는 현상

원본 링크

매개변수 W가 업데이트 되자 않아 학습이 되지 않음.

시그모이드 함수를 은닉층에 사용하는 것은 지양됨

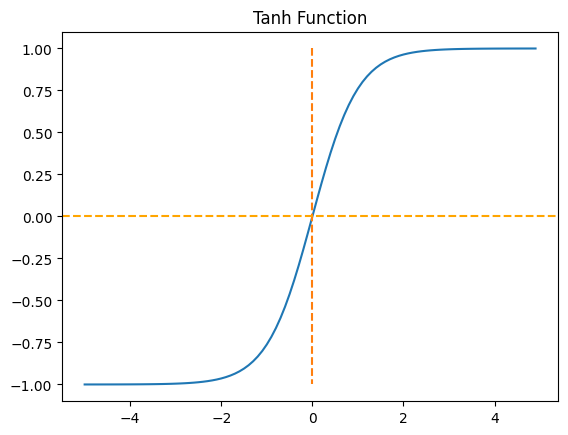
Hyperbolic Tangent Function

Hyperbolic Tangent Function

시그모이드 함수와 같은 문제가 발생함.
그러나 중심값이 0 >> 시그모이드 함수와 비교하면 반환값의 변화폭이 더 크다
>> 시그모이드 함수보다 기울기 소실이 적다 >> 은닉층에서 시그모이드 함수보다는 많이 사용된다.

Zero-centerd > 편향 이동 없음
입력의 절대값이 크면 -1 or 1로 수렴 > 기울기 소실 문제 발생 가능

원본 링크

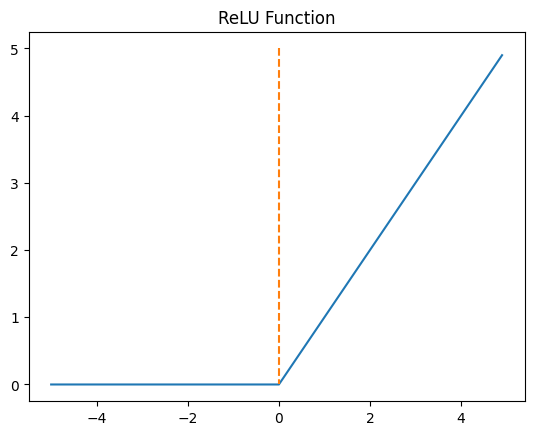
ReLU

ReLU

$f(x)=max(0,x)$

음수를 입력하면 0 을 출력, 양수를 입력하면 입력값을 그대로 반환.

특정 양수값에 수렴하지 않으므로 깊은 신경망에서 시그모이드 함수보다 훨씬 더 잘 작동
연산이 필요하지 않으므로 속도도 빠름
신경망 중간에 시그모이드함수 쓰는것보다는 무지성으로 ReLU 쓰는게 낫다

ReLU 로 선형함수의 출력 (렐루의 입력) 이 음수가 되어, 그 뉴런이 비활성화 된다고 해도 그게 항상 나쁜건 아님
오히려 필요없는 뉴런을 비활성화한다는 개념으로 이해해도 괜찮음.

Dying ReLU

입력값이 음수면 기울기0 >> 뉴런이 죽는다 >> 다시 회생시키기 어려움.

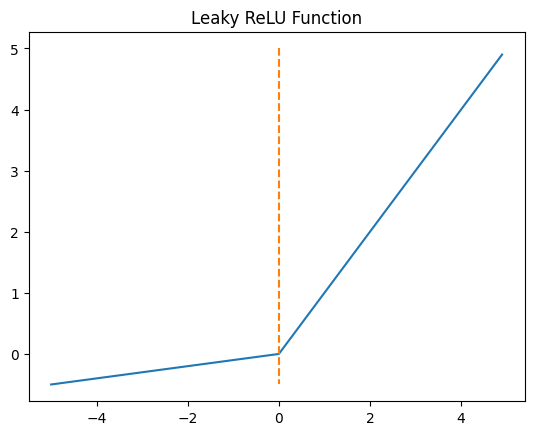
Leaky ReLU : 이 문제를 해결하기 위한 변형함수

원본 링크

원본 링크

Leaky ReLU

Leaky ReLU

$f(x)=max(ax,x)$
$a>0,a\approx 0$

원본 링크

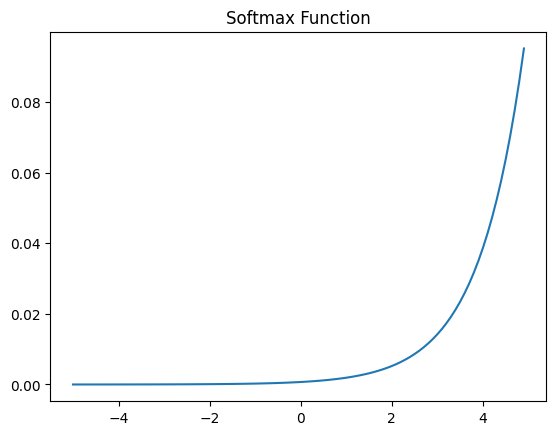
Softmax Function

Softmax Function

k차원의 벡터, i번째 원소를 $z_1$, i번째 클래스가 정답일 확률 $p_i$

$p_i=\frac{e^{z_i}}{{\sum }_{j=1}^k{e}^{z_j}}$

$softmax(z)=[\frac{e^{z_1}}{{\sum }_{j=1}^3{e}^{z_j}},\frac{e^{z_2}}{{\sum }_{j=1}^3{e}^{z_j}},\frac{e^{z_3}}{{\sum }_{j=1}^3{e}^{z_j}}]=[p_1,p_2,p_3]=\hat{y}=예측값$

원본 링크